Kuten blogin ensimmäisestä osasta muistetaan, binääriluokittelussa todellisten ja mallin antamien ennusteiden perusteella datajoukko voidaan luokitella neljään eri ryhmään. Merkitään jatkossa - yleisen käytännön mukaan - 0:lla negatiivista luokkaa ja 1:llä positiivista.
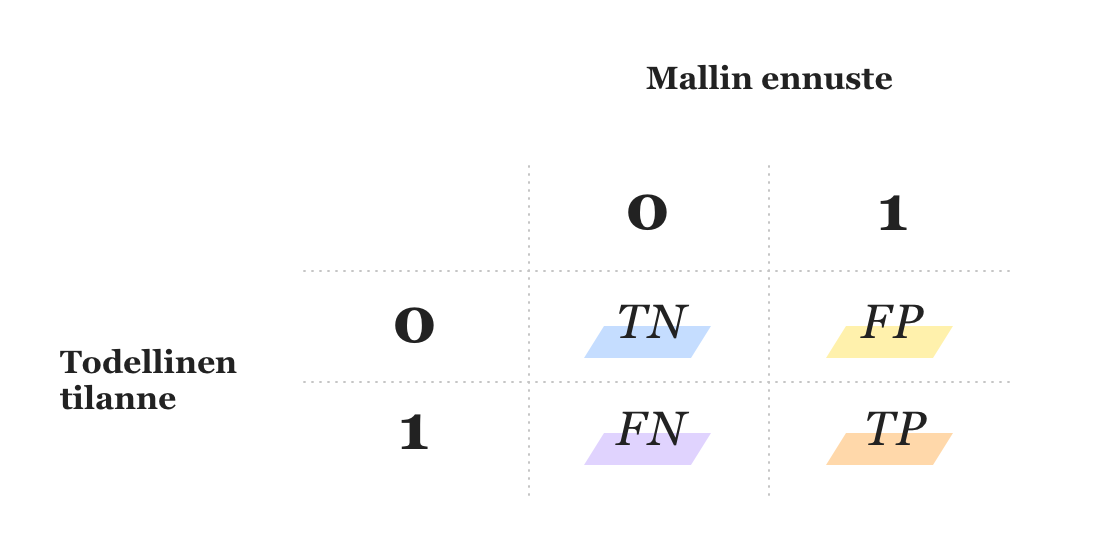
Yllä olevassa taulukossa TN = oikeat negatiiviset (true negative), FP = väärät positiiviset (false positive), FN = väärät negatiiviset (false negative), TP = oikeat positiiviset (true positive). Malli voi siis tehdä virheen kahdella tavalla: luokittelemalla negatiiviseen luokkaan kuuluvan datapisteen positiiviseksi (FP) tai positiiviseen luokkaan kuuluvan negatiiviseksi (FN).
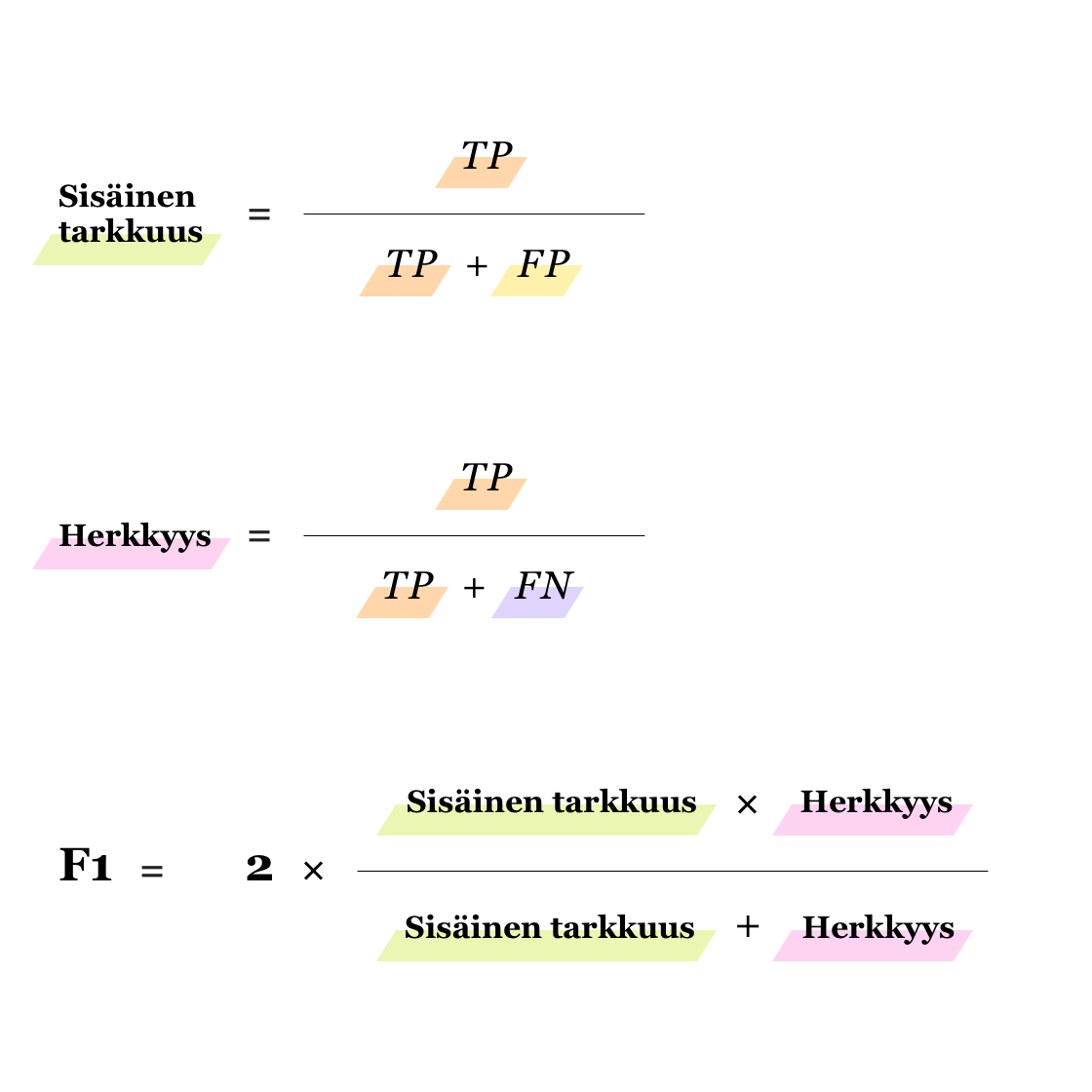
Binääriluokittelussa voidaan jokaiselle datapisteelle antaa pelkästään arvo 0 tai 1. Luokitteluun saadaan kuitenkin joustavuutta, jos pelkän nollan tai ykkösen sijaan ennustetaankin todennäköisyyttä jokaiselle datapisteelle. Tällöin jokainen datapiste saa arvon 0 tai 1 sijaan luvun väliltä (0,1). Tämä taas antaa mahdollisuuden asettaa itse kynnysarvo (threshold), jonka perusteella datapisteen luokka määritetään. “Luonnollinen” kynnysarvo on tietenkin 0.5, jolloin siis kaikki alle 0.5 todennäköisyyden saaneet datapisteet luokitellaan negatiivisiksi (luokka 0) ja sen ylittävät positiivisiksi (luokka 1).
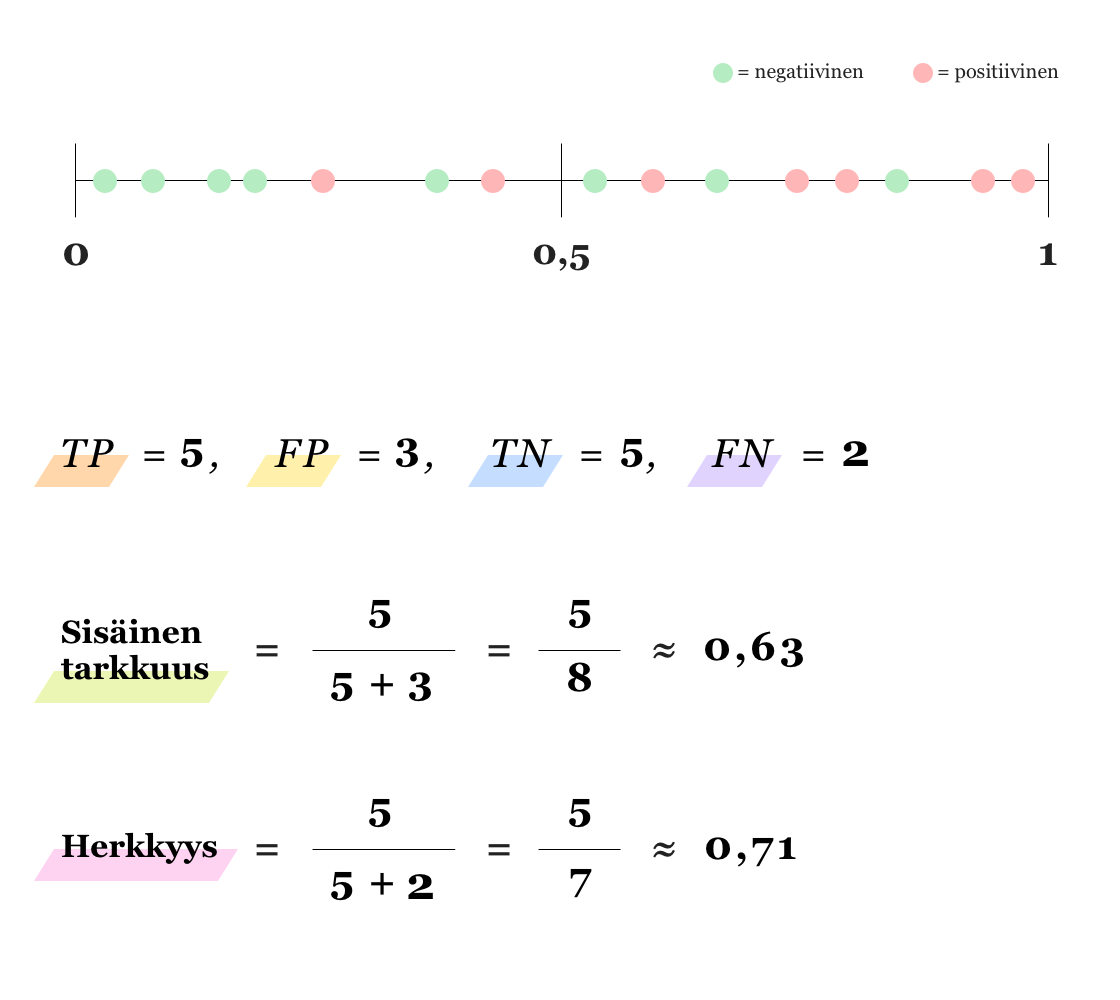
Riippuen siitä kumman virheen (FP vai FN) seuraukset ovat kriittisemmät, kynnysarvoa voi kuitenkin olla hyödyllistä siirtää jompaankumpaan suuntaan. Esimerkiksi sairauksien diagnosoinnissa on elintärkeää välttää vääriä negatiivisia, jotta kaikki sairaat henkilöt pääsevät hoitoon. Jos väärien positiivisten (FP) määrää halutaan vähentää (jolloin sisäinen tarkkuus kasvaa), kynnysarvoa täytyy nostaa, toisin sanoen datapiste tarvitsee suuremman todennäköisyyden tullakseen luokitelluksi positiiviseksi. Samoin, väärien negatiivisten määrä vähenee ja siten herkkyys kasvaa, jos kynnysarvoa lasketaan. Alla olevat kuvat valaisevat tilannetta (huomaa, että kyseessä on datapisteiden ja niiden todennäköisyyksien kannalta sama tilanne kuin yllä olevassa kuvassa).
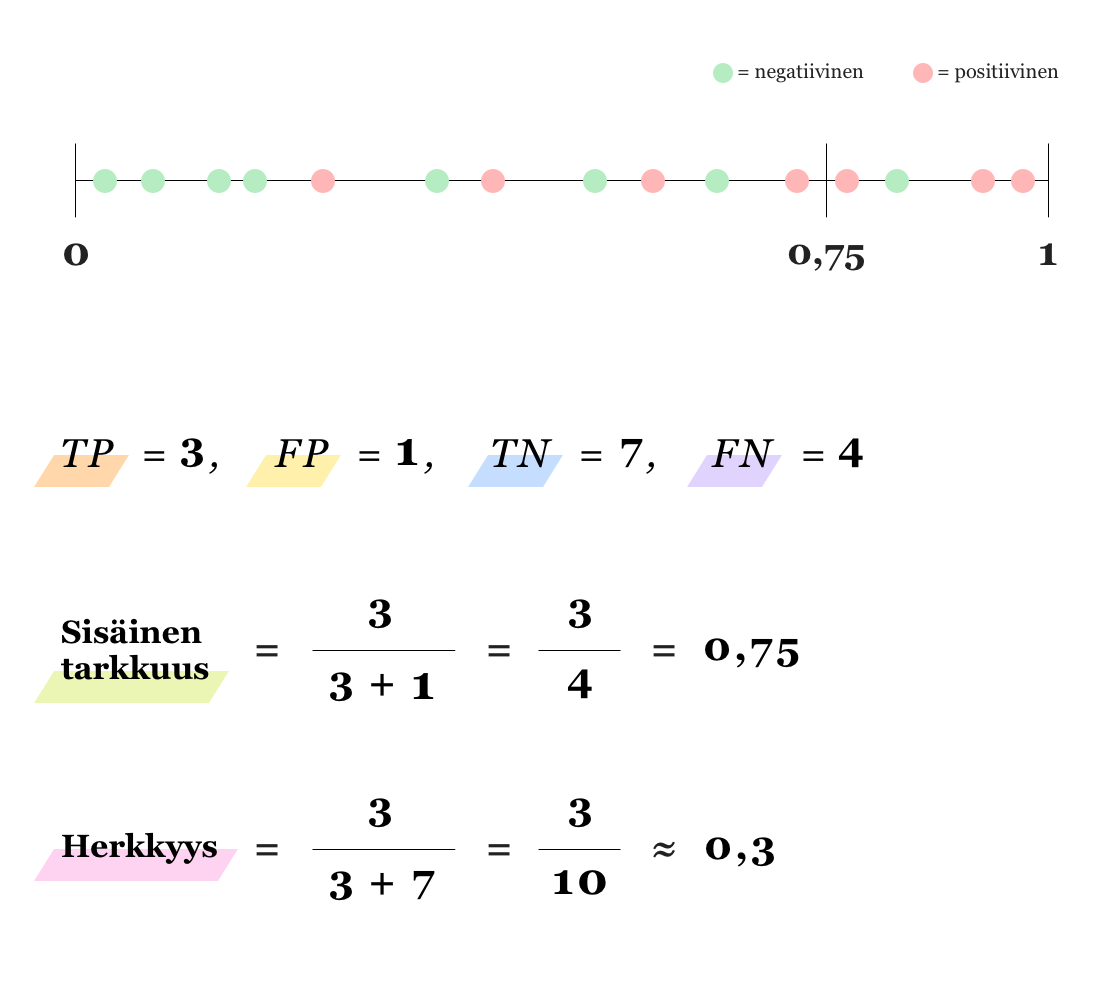

Kuten esimerkkikuviakin tarkastelemalla saattaa huomata, voi sekä sisäisen tarkkuuden että herkkyyden nostaminen yhtä aikaa olla mahdotonta. Tällöin onkin tärkeintä löytää hyvä tasapaino eli tilanne, jossa molemmat arvot ovat tarpeeksi hyviä. F1-arvo on hyvä mittari tähän, mutta se kertoo tilanteesta aina kiinnitetyllä kynnysarvolla. Mallin toimivuutta voi kuitenkin arvioida myös yli eri kynnysarvojen: voimme piirtää parametrisoidun käyrän koordinaatistoon, missä y-akselilla on sisäinen tarkkuus ja x-akselilla herkkyys (Precision-Recall Curve).
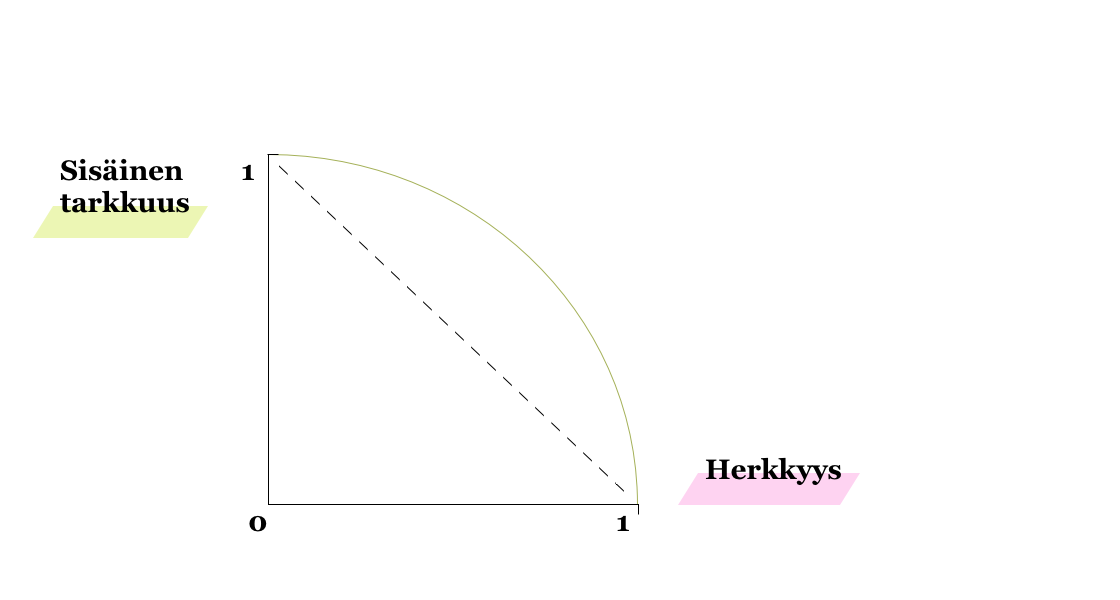
Kun kynnysarvo on 1.0 (eli 100 % datapisteistä luokitellaan negatiivisiksi), niin sisäinen tarkkuus on 1 ja herkkyys 0. Jos kynnysarvo on 0 eli kaikki datapisteet luokitellaan positiivisiksi, niin sisäinen tarkkuus on 0 ja herkkyys on 1. Mallin toimivuuden mittarina voidaan tässä käyttää pinta-alaa, joka jää käyrän alle; mitä parempi malli, sitä korkeammalla kuvaan piirretyn katkoviivan yläpuolella mallin käyrä on ja sitä lähempänä pinta-ala on arvoa 1.
Se, mikä sitten lopulta on tarpeeksi hyvä malli luokittelussa, ei siis ole lainkaan yksiselitteinen asia, vaan riippuu tutkittavasta ilmiöstä ja näkökulmasta. Tässä ja muissa data sciencen avulla ratkaistavissa haasteissa kannattaakin pitää mielessä, että mallin pitäisi lopulta olla vain ymmärryksen sivutuote.
