Nimensä mukaisesti luokittelu on pulmatehtävä, jonka tavoitteena on selvittää, mihin luokkaan annettu asia tai olio ominaisuuksiensa perusteella kuuluu. Esimerkiksi ihmisten kasvokuvia voidaan luokitella ilmeen perusteella tunnetilan mukaan neutraaleihin, iloisiin, surullisiin, vihaisiin ja yllättyneisiin. Binääriluokittelusta puhutaan, kun luokkia on täsmälleen kaksi. Esimerkiksi saapuvat sähköpostit voidaan luokitella roskapostiksi ja ei-roskapostiksi.
Kun luokiteltavia asioita ja niiden ominaisuuksia (eli datapisteitä) on enemmän kuin ihmisaivoilla jaksaa tai kannattaa laskea, voidaan luokittelussa hyödyntää koneoppimista. Luokitteluun soveltuvia klassisia algoritmeja ovat mm. päätöspuut ja logistinen regressio. Kuten kaikissa opetetuissa koneoppimismalleissa, myös luokittelussa on tärkeää arvioida mallin luotettavuutta ja tarpeen mukaan parantaa sitä. Usein ensimmäinen luonnollinen mittari tähän on sen ulkoinen tarkkuus (accuracy), joka kertoo, millä prosentilla malli luokittelee oikein. Reaalimaailmassa, jossa datajoukko on harvoin tasaisesti jakautunut, ulkoinen tarkkuus soveltuu kuitenkin huonosti binääriluokittelumallin arviointiin.
Esimerkki 1. Otetaan esimerkiksi tilanne, jossa halutaan estää luottokorttihuijaukset. Oletetaan, että luottokorttitapahtumia on 1000 kappaletta, joista 10 on huijauksia ja loput 990 rehellisiä tapahtumia. Pelkästään luokittelemalla kaikki tapahtumat rehellisiksi meillä on malli, jonka tarkkuus on 99 %! Valitettavasti tämä “malli” ei kuitenkaan onnistu poimimaan ollenkaan huijauksia, joiden tunnistamiseksi malli haluttiin.
Esimerkki 2. Oletetaan, että meillä on malli, joka verikokeiden tulosten ja oireiden perusteella luokittelee ihmiset terveisiin (negatiivinen diagnoosi) ja sairaiksi (positiivinen diagnoosi). Mallia testataan 100 ihmisen otoksella, joista 10 tiedetään sairaiksi. Malli antaa seuraavat tulokset:

Siis 10 sairaasta viisi on luokiteltu oikein (oranssi) ja viisi taas väärin (lila). Kaikki 90 tervettä malli onnistui luokittelemaan oikein. Malli osuu ennustuksissaan oikeaan siis 95 % (ulkoisella) tarkkuudella. Mutta puolet sairaista saa tämän mallin mukaan terveen diagnoosin, joten mallia ei voi pitää hyvänä.
Sisäinen tarkkuus ja herkkyys
Binääriluokittelussa datapisteet voi siis jakaa neljään ryhmään:
- Oikeat positiiviset eli ne positiiviset, jotka malli ennusti positiivisiksi (oranssi)
- väärät positiiviset eli ne negatiiviset, jotka malli ennusti positiivisiksi (keltainen)
- oikeat negatiiviset eli ne negatiiviset jotka malli ennusti negatiivisiksi (sininen)
- väärät negatiiviset eli ne positiiviset, jotka malli ennusti negatiivisiksi (lila)
Ulkoisen tarkkuuden sijaan binääriluokittelussa mallin luotettavuudesta kertookin paremmin sisäinen tarkkuus (Precision) tai herkkyys (Recall, Sensitivity, True Positive Rate).
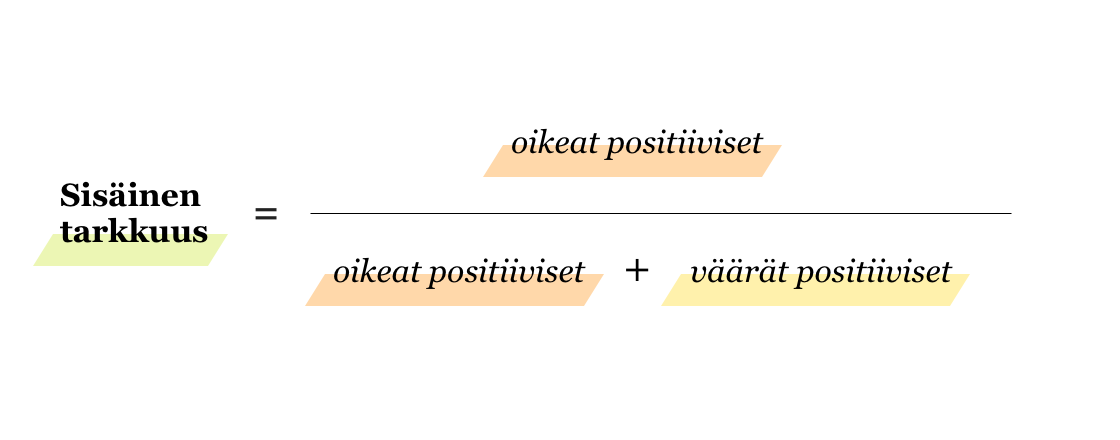
Sisäinen tarkkuus kertoo siis, kuinka suuri osuus kaikista positiivisiksi luokitelluista datapisteistä oikeasti oli positiivisia. Koska tärkeiden sähköpostien ei haluta menevän roskapostiin, on niiden luokittelussa tärkeää, että sisäinen tarkkuus on suuri (pieni väärien positiivisten osuus).
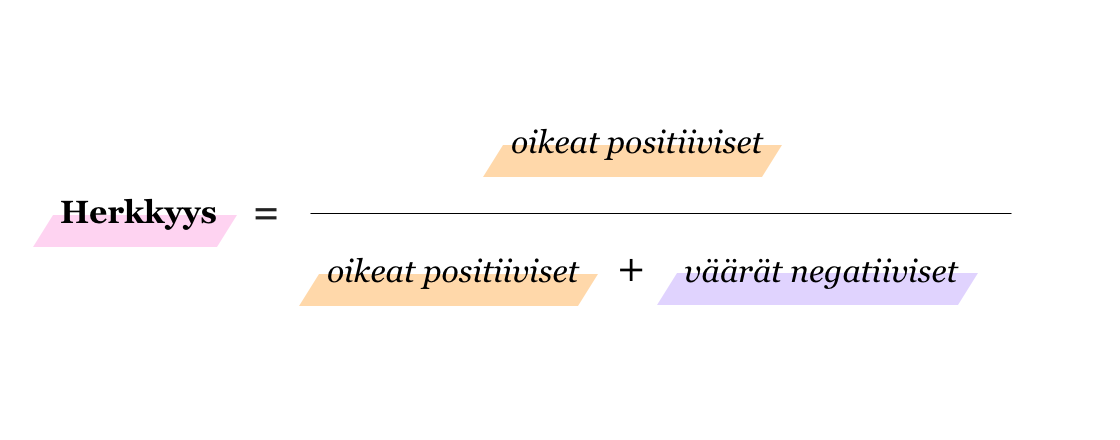
Herkkyys taas kuvaa, miten hyvin malli onnistuu luokittelemaan positiivisiksi kaikki oikeasti positiiviset tapaukset. Vaarallisten ja tarttuvien tautien diagnooseissa on tärkeää, että väärien negatiivisten osuus on mahdollisimman pieni, joten mallille halutaan suuri herkkyys. Esimerkin 2 tapauksessa mallin herkkyys on vain 5/(5+5) = 0.5 eli 50%. Vaikka sen sisäinen tarkkuus on 5/(5+0)=1.0 eli 100%, se ei tässä tapauksessa - seuraukset huomioon ottaen - ole lainkaan hyvä mittari mallin luotettavuudelle.
Esimerkiksi luottokorttihuijauksissa on toki tärkeää poimia väärinkäytökset, mutta toisaalta rehellisiä tapahtumia ei haluta turhaan luokitella huijauksiksi. Kumpaan mittariin, sisäiseen tarkkuuteen vai herkkyyteen, tällaisissa tapauksissa keskittyä? Toisaalta halutaan ehdottomasti välttää vääriä negatiivisia (korkea herkkyys), mutta myöskään väärät positiiviset eivät ole toivottuja (korkea sisäinen tarkkuus). Apuna sisäisen tarkkuuden ja herkkyyden välisen tasapainon löytämiseksi voi käyttää niin sanottua F1-arvoa, joka on näiden harmoninen keskiarvo:

Lisää tästä sisäisen tarkkuuden ja herkkyyden vaihtokaupasta sekä todennäköisyyden hyödyntämisestä ennusteissa blogin seuraavassa osassa.